Art and Science in Dialogue

Art and Science in Dialogue Art and Science in Dialogue

BACKGROUND

PROJECT INFO

An elegant example of the connections between science and the creative disciplines is demonstrated in the parallels between crystallography (the study of crystal structures) and pattern design.

Crystals are made up from a regular arrangement of identical units. Each unit contains one or more molecules, packed together in a symmetrical way. In a similar manner, the design of repeating patterns rely on the creation of motifs, which repeat in a symmetrical way.

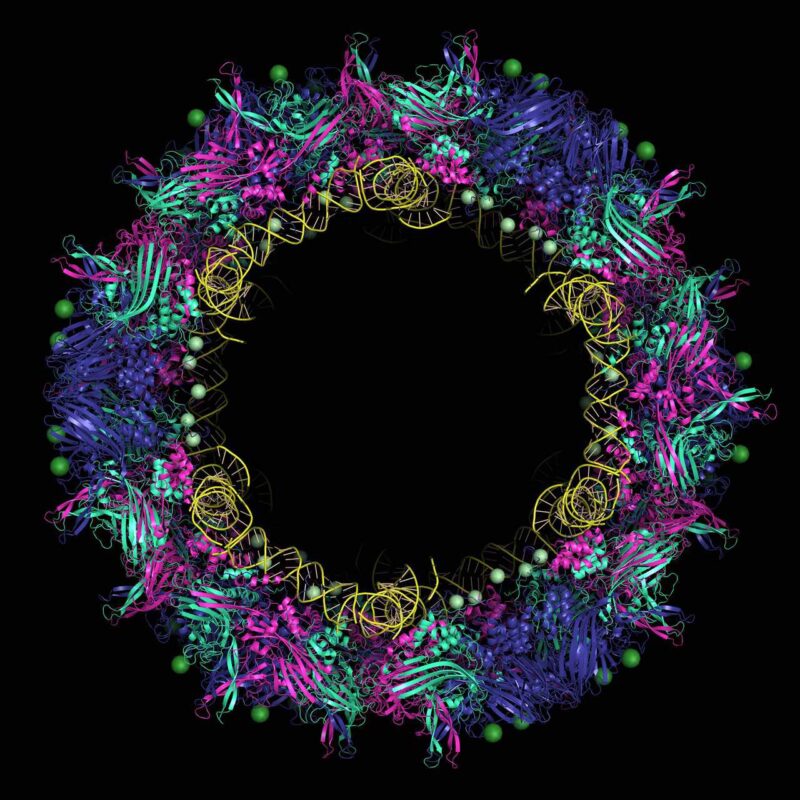
The use of X-ray crystallography as a method for determining the complex structure of proteins and other biological molecules has enabled the study of large macromolecular assemblies such as viruses.

From the images under the microscope, the concept of visualising the geometry of viruses evolved. In particular, nested and expandable polyhedra provide new insights into viral architecture. The process of exploring their visual representation has resulted in the design of polyhedral models, providing  mathematical insights and tools for the communication of science.

Year

2014 – 2015

Collaborators

Reidun Twarock (York), Scientific Direction
Emilio Zappa (York), Postgraduate Researcher
Moteijus Valiunas (Cambridge), Undergraduate Researcher
Adam Arstall (Oxford), Undergraduate Researcher

Funders

Centre for Chronic Diseases and Disorders (C2D2)
Holbeck Charitable Trust
University of Leeds
University of York
Wellcome Trust

EXPANDOHEDRA

A large class of viruses undergo a maturation process that involves an expansion of the capsid (or protein shell). Many open questions remain about the way this process works. 

A visual representation of the mechanism of the expansion of a virus is possible through expandohedra. These consist of pentagons attached by rigid rods, which represent protein links. The connecting rods enable the pentagons to rotate with a certain freedom, creating a visualisation of the asymmetric expansion.

NESTED POLYHEDRA

Inspired by the structures of viruses and fullerenes in biology and chemistry, we constructed a class of nested polyhedra as double shell structures. These provide blueprints for simple viral capsids to help predict information about its structure (for example capsid thickness).

The vertices of the outer shell describe the location of the capsid proteins, whereas the inner shell gives information on the genomic material (RNA) inside the capsid. We visualised sections of two viral capsids matched to nested shells: Bacteriophage MS2 and Pariacoto virus.

GALLERY

This project was first showcased alongside the international Mathematical Virology Workshop in August 2014 and presented as the exhibition ‘Viruses, Patterns and Polyhedra: Art and Science in Dialogue’. 

"The exhibition and gallery talk at this meeting were a particular treat. I think all of us are drawn aesthetically by the symmetry and deviations in viruses. Seeing this represented in beautiful life sized objects struck a deep chord in me."

Professor Prevelige, Department of Microbiology, University of Alabama at Birmingham
Following the success of the ‘Viruses, Patterns and Polyhedra’ exhibition in 2014, we continued to develop further creative visualisations. These were exhibited both nationally and internationally:
  • ‘Visualisations in Mathematical Virology’ in the C2D2 showcase at City Screen, York, UK (March–April 2015)
  • ‘Viruses: Mathematical Visualisations’ as part of York Festival of Ideas, York, UK (June 2015)
  • in MathArt, College of Fine Arts, Towson University, Maryland, Baltimore, USA (June–July 2015)
  • in the Bridges Exhibition of Mathematical Art, University of Baltimore, USA (July–August 2015)

YORK FESTIVAL OF IDEAS, 2015

PUBLIC TALKS & OUTREACH WORKSHOPS

Our work was shared through a number of workshops and science fairs including as part of the health zone at of EU Researcher’s Night (York, September 2014) and Leeds Festival of Science (March, 2015). Pull-up nets from these workshops – created with patterns based on viral capsid triangulation (T) numbers – are available from the Resources page.

Through public talks as part of the programmes for Pint of Science (York, May 2015) and York Festival of Ideas (June, 2015), we shared insights into the interdisciplinary dialogue and process of working between scientist and designer.

SELECTED PUBLICATIONS, POSTERS & EXHIBITIONS

Download
Thomas, B., Twarock, R., Valiunas, M. and Zappa, E. (2015). “Nested Polytopes with Non-crystallographic Symmetry Induced by Projection,” in Bridges Conference Proceedings 2015, pp.167—174.
Download
Arstall, A., Thomas, B., Twarock, R. and Zappa, E. (2015). “Expandohedra: Modeling Structural Transitions of a Viral Capsid,” in Bridges Conference Proceedings 2015, pp.471—474.
Download
Thomas, B. in collaboration with the Twarock group (2015). “Viruses: Mathematical Visualisations.” York Festival of Ideas, Ron Cooke Hub, York, 8–12 June 2015.
 
Download
Arstall, A., Zappa, E., Cermelli, P., Indelicato, G., Thomas, B. and Twarock, R. (2014). “Expandable Polyhedra: A Mechanical Way to Model Structural Transitions of Viral Capsids.” Mathematical Virology Workshop 2014.
 
Download
Valiunas, M., Zappa, E., Thomas, B. and Twarock, R. (2014). “Beyond Caspar-Klug Theory: Nested Polyhedra as a Predictive Tool for Virus Architecture.” Mathematical Virology Workshop 2014.